CNN
1. Concept
Applying ’translation invariance’ and ’locality’ to the MLP, we then get a CNN which can significantly reduce the parameters.
$$h_{i,j} = \sum_{a,b}v_{i,j,a,b}x_{i+a,j+b}$$
$$\Rightarrow h_{i,j} = \sum_{a=-\Delta}^{\Delta}\sum_{b=-\Delta}^{\Delta}v_{a,b}x_{i+a,j+b}$$
2. Conv2d
2.1 Definition
-
Input $$X: (N, C_{in}, H, W)$$
-
Kernel $$W: (h,w)$$
-
Bias: $$b$$
-
Output $$Y: (N, C_{out}, H’, W’)$$
$$Y=X\star W+b$$
2.2 Cross Correlation
$$y_{i,j} = \sum_{a=1}^{h}\sum_{b=1}^{w}w_{a,b}x_{i+a,j+b}$$
2.3 Conv2d
$$y_{i,j} = \sum_{a=1}^{h}\sum_{b=1}^{w}w_{-a,-b}x_{i+a,j+b}$$
As for implementation, we use ‘Cross Correlation’ but call it ‘Conv2d’.
2.4 Conv1d && Conv3d
text, language, time sequences.
$$y_{i} = \sum_{a=1}^{h}w_{a}x_{i+a}$$
videos, medical images, meteorology.
$$y_{i, j, k} = \sum_{a=1}^{h}\sum_{b=1}^{w}\sum_{c=1}^{d}w_{a,b,c}x_{i+a,j+b,k+c}$$
inception v1…
3. Padding
While using Conv2d, we usually get smaller features. In order to keep the shape constant, we fill 0s at the edge.
Output Shape: $$(H, W) => (H-h+p_h+1,W-w+p_w+1)$$
Normally we choose $$p_h = h-1, p_w = w-1$$, then the shape doesn’t change.
If h is odd, then padding $$\frac{p_h}{2}$$ on both sides, otherwise, we padding $$\lfloor \frac{p_h}{2} \rfloor$$ and $$\lceil \frac{p_h}{2} \rceil$$.
4. Stride
While using Conv2d, sometimes we hope to decrease the shape faster. What we can do is to increase the stride of each move.
Output Shape: $$(H, W) => (\lfloor\frac{H-h+p_h+s_h}{s_h}\rfloor,\lfloor\frac{W-w+p_w+s_w}{s_w}\rfloor)$$
If $$p_h = h-1, p_w = w-1$$, and we know that $$\frac{s_h-1}{s_h}<1$$, then the output is $$(\lfloor\frac{H}{s_h}\rfloor,\lfloor\frac{W}{s_w}\rfloor)$$
the essence of ml is compression!
5. Channel
Each channel has a corresponding kernel, and the result is the sum of them.
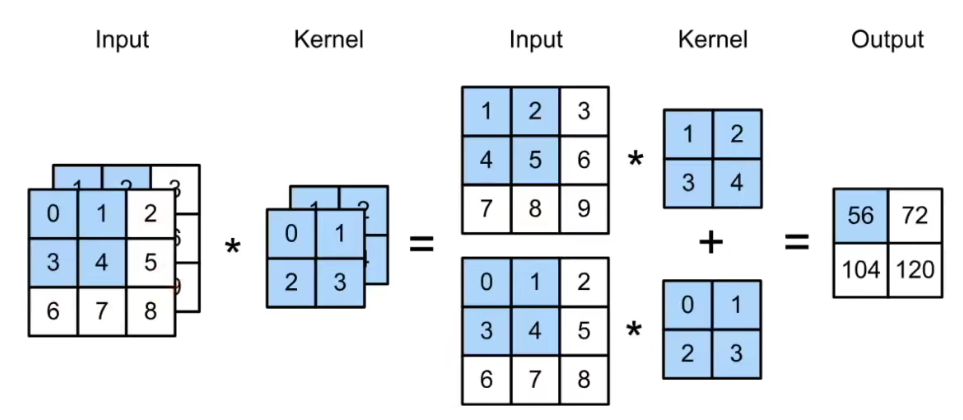
5.1 Input channel
-
input: $$X: C_{in},H,W$$
-
kernel: $$W: C_{in},h,w$$
-
output: $$Y: H’,W’$$
$$Y=\sum_{i=0}^{C_{in}}X_{i,:,:}\star W_{i,:,:}$$
5.2 Output channel
Output channel can be regarded as patterns that we want to recognize. For MNIST, we gradually increase the number of channels and obtain the textures of these images, then compress these information into the ‘class label’ of each image by MLP.
-
input: $$X: C_{in},H,W$$
-
kernel: $$W: C_{out},C_{in},h,w$$
-
output: $$Y: C_{out},H’,W’$$
5.3 1x1 Kernel
It’s equivalent to a Full Connected Layer, and each kernel fuse channels by sharing parameters. No space pattern.
5.4 Complexity
$$O(C_{in}C_{out}hwH’W’)$$
‘padding 0’ only add a constant to the result.
6. Pooling Layer
Edge detecton [1, -1] is position sensitive. So ‘Pooling Layer’ add transform invariance which return the maximum(average) of the sliding window. In general, Max and Avg has no difference, but Avg data doesn’t appear in original data.
6.1 features
- hyperparameter: size, padding, stride(=size by default)
- no learning parameter
- input channel + pooling layer => output channel
- output channel = input channel (no channel fuse)
6.2 Q&A
The ‘data transform’ play down its role. cnn visualization.. transfer learning..