1. Classification Problem

Supposed that we are given a batch of data $$D={(x_1, y_1), (x_2, y_2), …, (x_m, y_m)},y_i \in {-1,+1}$$, and we want to find a hyper-plane such that it can properly divide these two class of data. A good hyper-plane should be able to accept slight disturbance.

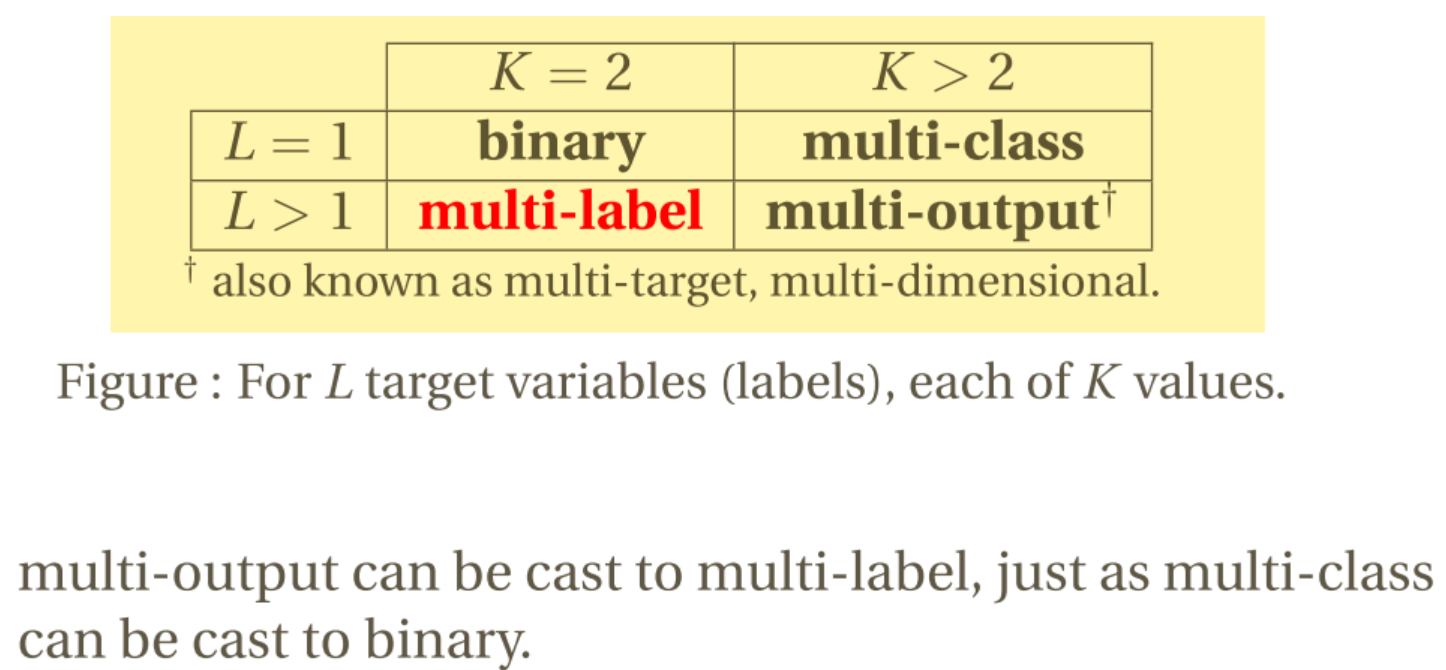
Multi-class Classification

A classification task with the assumption that each sample belongs to one and only one class. $${dog, cat}$$

Multi-label Classification

A classification task that handle several joint classification tasks. $${cat, young, female}$$

2. Mathematical Description

2.1 Hyper-plane

We use ${w, b}$ to describe a hyper-plane in n-dimension vector space, where $w=[w_1, w_2, …, w_n]^T$ is the normal vector and $b$ is the displacement vector. The mathematical equation of the hyper-plane is

$$ w_1x_1+w_2x_2+…+w_nx_n+b=0 $$

2.2 Distrance & Sign

To derive the distance of any sample $x=[x_1, x_2, …, x_n]^T$ to the hyper-plane ${w, b}$, we can first find a point $(-\frac{b}{w_1},0, …, 0)$ in this hyper-plane. To connect $x$ and this point, we get a new vector

$$ n=[x_1+\frac{b}{w_1},x_2,…,x_n]^T $$

Next, we can get the distance of $x$ to this hyper-plane by using the projection formula.

$$r=\frac{|w^Tn|}{||w||}=\frac{\vert w^Tx+b\vert}{\lVert w\rVert}$$

The sign of $w^Tx+b$ depends on the position $x$ with respect to the hyper-plane. If $x$ is in the side that $w$ points to, the result is negative. Otherwise, the result is positive.

2.3 Hard Margin

We hope that this hyper-plane can seperate these two class of samples with margins greater than $\frac{1}{\lVert w\rVert}$. This can be expressed as

$$\begin{cases} w^Tx_i+b\ge +1, ~ y_i=+1; \ w^Tx_i+b\le -1, ~ y_i=-1. \end{cases}$$

Therefore the classification problem is equivalent to

$$\max_{w,b}\frac{2}{\lVert w\rVert} ~~ s.t. ~~ y_i(w^Tx_i+b)\ge 1,\xi_i \gt0, ~~ \forall i=1,2,…,m$$

Here, $\frac{2}{\lVert w\rVert}$ is called the margin (间隔), which is supposed to be as great as possible.

This kind of margin is called “hard margin” which means that the samples are strictly outside the boundaries.

2.4 Soft Margin

Soft margin is another type of SVM margin, which accepts error　$\xi=[\xi_1,\xi_2, …, \xi_m]^T$. The condition can be written as

$$\min_{w,b,\xi} \bigg[ \frac{\lVert w\rVert}{2}+C\sum_{i=1}^{m}\xi_i \bigg] ~~ s.t. ~~ y_i(w^Tx_i+b)\ge 1-\xi_i, ~~ \forall i=1,2,…,m$$

$C>0$ is a hyper-parameter that is used to adjust the error tolerance. The greater the $C$, the closer the error $\xi$ to zero.?

3. Dual Problem (对偶问题)

By Lagrange Multiplier Method, we can construct the Lagrange function,

$$L(w,b,a) = \frac{\vert\vert w \vert\vert^2}{2} + \sum_{i=1}^{m}a_i(1-y_i(w^Tx_i+b))$$

By setting the derivatives to zero, we have

$$w=\sum_{i=1}^{m}a_iy_ix_i,\ 0=\sum_{i=1}^{m}a_iy_i$$