1. Dichotomy

def sqrt(x, e=1e-6):
    if x<0:
        return -1 # error
    if x==0:
        return 0

    if x < 1:
        a, b = x, 1
    else:
        a, b = 0, x

    while b-a > e:
        m = (a+b)/2
        if m*m > x:
            b = m
        else:
            a = m
    return (a+b)/2

Time complexity:

$$ \frac{x}{2^{f(n)}} < e \ f(n) > log2(x/e) $$ Since e is usually a fixed number, the time complexity is $O(log(x))$

2. Newton’s method

def sqrt(x, e=1e-6):
    y = x # initial guess
    while abs(y*y-x) > e:
        y = (y + x/y)/2
    return y

Proof

We define $f(x) = x^2 - c$ and try to find the square root of c.

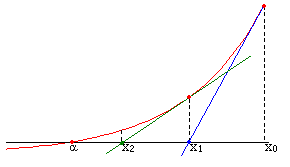
In the beginning, we guess $x_0$. And draw a tangent line to $f(x)$ at $x_0$.

$$\begin{aligned} g(x) &= f(x_0) + f’(x_0)(x-x_0) \\ &= x_0^2 - c + 2x_0(x-x_0) \\ &= 2x_0x - x_0^2 - c \end{aligned}$$

The tangent line intersects the $x$-axis at $x_1$.

$$ x_1 = (x_0 + \frac{c}{x_0})*0.5 $$